De richtingscoëfficiënt: richting en steilheid van een lijn.
Betekenis
De richtingscoëfficiënt is ingewikkeld en abstract begrip, zeker als je het de eerste keer leest of hoort. Bovendien is het woord samengesteld! Samengesteld betekent dat het woord is ‘gemaakt’ door twee worden aan elkaar te plakken; in dit geval ‘richting’ en ‘coëfficiënt’ . Richtingscoëfficiënt is makkelijker te begrijpen door de betekenis van de woorden, richting en coëfficiënt. Het woord richting spreekt voor zich: ”Hij ging naar links of rechts”. Het woord coëfficiënt is wat lastiger, het is een ‘duur’ woord voor getal. Het begrip richtingscoëfficiënt is dus een getal dat iets zegt over de richting en steilheid van een lijn.
Naast het begrip richtingscoëfficiënt wordt ook het begrip ‘hellingsgetal’ gebruikt. Maar dat is lood om oud ijzer omdat dit een typisch gevalletje van ‘namedropping’ is.
Role of slope in mathematics.
Zoals Sint en Piet bij elkaar horen zo hoort in de wiskunde de richtingscoëfficiënt bij het lineaire (lijn) verband. De algemene formule van een lineair verband of lijn is: ƒ(x) = ax + b. Door aan de letters a en b een waarde toe te kennen, bijvoorbeeld a=3 en b= 7, krijg je een specifieke lijn: ƒ(x) = 3x + 7. Het getal dat voor de x staat, het getal 3, is de richtingscoëfficiënt van de lijn. Zoals eerder staat vermeld, is de richtingscoëfficiënt een getal dat informatie geeft over het verloop of richting van de lijn. Er zijn vier soorten lijnen: 1) stijgende lijnen 2) dalende lijnen 3) de horizontale lijn en tot slot 4) de verticale lijn. In onderstaande figuur zijn de vier soorten lijnen terug te zien.
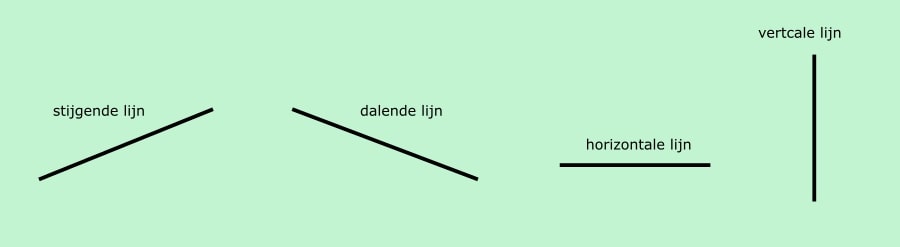
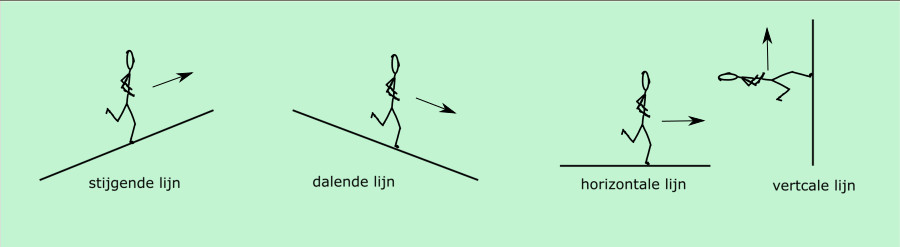
De horizontale lijn en de verticale lijnen spreken voor zich. Stijgen en dalen heeft wat uitleg nodig. Net zoals je van links naar rechts leest zo lees en kijk je ook bij wiskunde. De leesrichting is bepalend of je een lijn stijgend of dalend noemt. “Loop” je van links naar rechts en ga je omhoog dan is de lijn stijgend, de helling van de weg loopt omhoog. Een manier om het te onthouden, kan door een mannetje op de lijnen te tekenen. Je ziet dan zelf of dit mannetje omlaag of ophoog loopt.
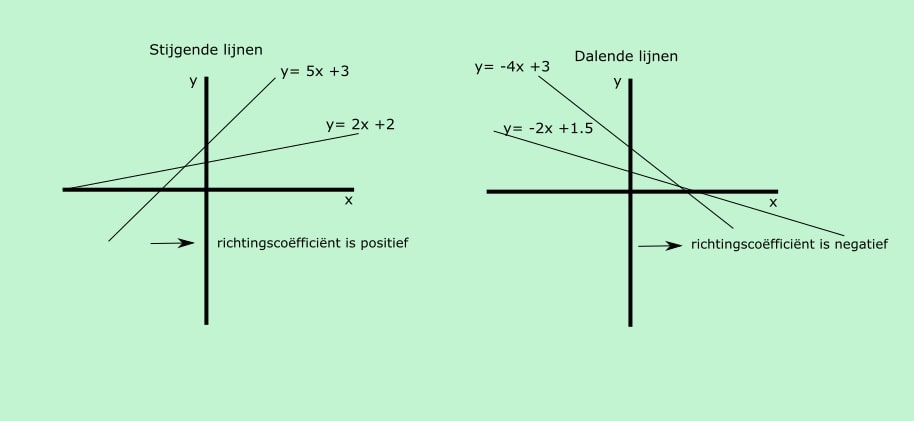
Nu je weet wanneer een lijn daalt en stijgt kunnen we dat koppelen aan de richtingscoëfficiënt van de lijn. Als een lijn stijgt dan is de richtingscoëfficiënt altijd een positief getal, zie onderstaande figuur. Is de richtingscoëfficiënt een negatief getal dan daalt de lijn. (Een horizontaal heeft een richtingscoëfficiënt gelijk aan nul. Een verticale lijn heeft geen richtingscoëfficiënt).
 Calculating the slope.
Calculating the slope.
Hoe je de richtingscoëfficiënt van een lijn kunt berekenen, kun je op veel wiskundesites en youtube terugvinden. De uitleg die ik zou geven wijkt niet veel af van alles dat op internet staat. Het enige dat eventueel een aanvulling zou kunnen zijn is de volgorde waarin ik de uitleg zou geven.

Would you like to experience how it feels to take tutoring for math, stats or physics at MathMind? Then try a free trial lesson. For questions, please contact Sjuup Rekko.